The proposed optimized multi agent reinforcement learning for average localization error prediction is presented in this section. Accurate sensor node position estimation is required in WSNs for efficient operation. Factors like environmental noise, limited transmission ranges, and irregular node placements introduce deviation between the estimated position and its actual position. This deviation is quantified as Localization Error (LE). On an average it is mentioned as ALE which defines the LE across all sensor nodes in a WSN. Mathematically average localization error is formulated as
$$\:LE=\frac{1}{N}{\sum\:}_{i=1}^{N}|\widehat{{P}_{i}}-{P}_{i}|$$
(1)
where \(\:LE\) indicates the average localization error, \(\:N\) indicates the total sensor nodes, \(\:\widehat{{P}_{i}}\) indicates the predicted position of the \(\:{i}^{th}\) node which is represented as a coordinate vector \(\:\left(\widehat{{x}_{i}},\widehat{{y}_{i}}\right)\). \(\:{P}_{i}\) represents the actual position which is represented as a coordinate vector \(\:\left({x}_{i},{y}_{i}\right)\), \(\:|\cdot\:|\) indicates the Euclidean norm which is calculated as follows
$$\:|\widehat{{P}_{i}}-{P}_{i}|=\sqrt{{\left(\widehat{{x}_{i}}-{x}_{i}\right)}^{2}+{\left(\widehat{{y}_{i}}-{y}_{i}\right)}^{2}}$$
(2)
Based on the above, LE for each node and its average across all nodes in the WSN are obtained. The smaller values of \(\:LE\) indicates the estimated positions are close to the true positions indicating better localization accuracy. Though minimizing the average localization error \(\:LE\) is essential, it is equally important to ensure that the error is consistent across all nodes. High variability in localization error among nodes leads to unreliable networks and affects the overall performance. To address this the Standard Deviation of Localization Error \(\:S{D}_{LE}\) is introduced. The standard deviation measures the variability of localization errors which are mathematically formulated as
$$\:S{D}_{LE}=\sqrt{\frac{1}{N}{\sum\:}_{i=1}^{N}{\left(|\widehat{{P}_{i}}-{P}_{i}|-LE\right)}^{2}}$$
(3)
where \(\:S{D}_{LE}\) indicates the standard deviation of localization error which captures the deviations of errors around the mean \(\:LE\), \(\:|\widehat{{P}_{i}}-{P}_{i}|\) indicates the localization error of the \(\:{i}^{th}\) node. \(\:LE\) indicates the mean localization error which is obtained by taking the average of individual localization errors. A lower \(\:S{D}_{LE}\) indicates more consistent localization performance across all nodes.
The major WSN parameters which affect the localization are transmission range, anchor ratio, node density, and algorithm iterations parameters. The anchor Ratio \(\:{A}_{r}\) is defined as the proportion of anchor nodes to the total number of nodes in the network. A higher anchor ratio improves localization accuracy due to the availability of more reference points. The Transmission Range \(\:{T}_{r}\) is defined as the maximum distance within which nodes can communicate. The larger transmission ranges reduce communication gaps but it increases signal interference which will affect the accuracy. The node density \(\:{N}_{d}\) is defined as the number of nodes per unit area. The higher densities enhance accuracy by increasing the node connectivity and reducing localization uncertainty. Iterations \(\:{I}_{t}\) defines the number of iterations in the localization process. More iterations improve convergence to accurate estimates. These parameters collectively define the state of the WSN which is mathematically represented as
$$\:{S}_{t}=\left[{A}_{r},{T}_{r},{N}_{d},{I}_{t}\right]$$
(4)
where \(\:{S}_{t}\) indicates the state at time \(\:t\). Accurately predicting \(\:LE\) and minimizing its value requires understanding and optimizing these parameters. Thus, the primary objective is to predict and minimize \(\:LE\) while reducing \(\:S{D}_{LE}\) for reliable localization in WSNs. Mathematically, the problem is formulated as
$$\:Minimize\:LE\left({S}_{t}\right)\:and\:S{D}_{LE}\left({S}_{t}\right)$$
(5)
subject to
$$\:{{A}_{r}}_{min}\le\:{A}_{r}\le\:{{A}_{r}}_{max}\:{{T}_{r}}_{min}\le\:{T}_{r}\le\:{{T}_{r}}_{max}\:{{N}_{d}}_{min}\le\:{N}_{d}\le\:{{N}_{d}}_{max}\:{{I}_{t}}_{min}\le\:{I}_{t}\le\:{{I}_{t}}_{max}\:\}$$
(6)
where \(\:min\) and \(\:max\) indicates the allowable parameter ranges for transmission range, node density, anchor ratio, and iterations. These constraints ensure that the network operates within practical and feasible limits.
Multi-Agent reinforcement learning (MARL) algorithm
The proposed MARL framework utilizes multiple agents, each responsible for adjusting specific WSN parameters (e.g., anchor ratio, transmission range, node density) to minimize Average Localization Error (ALE). The multi-agent behavior is designed as a decentralized learning system, where each agent independently explores actions based on its local state while receiving a global reward reflecting the overall ALE reduction. Knowledge sharing occurs through a centralized Q-value function during training, where agents share their experiences (state-action-reward transitions), enabling the model to learn collective patterns and refine policies for better coordination.
The convergence of agents is achieved using an epsilon-greedy policy combined with the Bellman equation for Q-value updates. Convergence is confirmed when the Q-values stabilize, and the difference between consecutive policy updates falls below a predefined threshold, ensuring that agents have collectively learned an optimal policy for minimizing ALE. The integration of GJO further accelerates convergence by optimizing MARL hyperparameters (e.g., learning rate and reward weights), ensuring efficient exploration and exploitation. This collaborative learning mechanism enables the proposed model to adapt dynamically and achieve superior localization accuracy in WSN environments.
The MARL is the major element of the proposed model for adaptively predicting and minimizing ALE in WSNs. The proposed MARL has states, actions, and reward functions. The state \(\:{S}_{t}\) captures the characteristics of the WSN at time \(\:t\). It includes the critical parameters that influence localization error \(\:{S}_{t}\). To ensure uniform scaling and improve learning efficiency the parameters are normalized which are mathematically formulated as follows
$$\:{S}_{t}^{norm}=\frac{{S}_{t}-\mu\:}{\sigma\:}$$
(7)
where \(\:\mu\:\) indicates the mean of each parameter across the dataset, \(\:\sigma\:\) indicates the standard deviation of each parameter. \(\:{S}_{t}^{norm}\) indicates the normalized state and ensures all features present in the comparable range. The state \(\:{S}_{t}^{norm}\) is used as input to the MARL so that the current condition of the WSN is obtained. The action \(\:{A}_{t}\) indicates the decisions made by the agents at time \(\:t\) to modify WSN parameters dynamically. Each agent adjusts one or more parameters. Mathematically the action vector is expressed as
$$\:{A}_{t}=\left[\varDelta\:{A}_{r},\varDelta\:{T}_{r},\varDelta\:{N}_{d},\varDelta\:{I}_{t}\right]$$
(8)
where \(\:(\varDelta\:{A}_{r},\varDelta\:{T}_{r},\varDelta\:{N}_{d},\varDelta\:{I}_{t})\) indicates the changes in transmission range, anchor ratio, node density, and iterations, respectively. The range of actions is controlled to ensure that adjustments remain within the limits which are formulated as
$$\:{A}_{t}\in\:\left[{\varDelta\:}_{min},{\varDelta\:}_{max}\right]$$
(9)
where \(\:{\varDelta\:}_{min}\) and \(\:{\varDelta\:}_{max}\) indicates the minimum and maximum allowable adjustments for each parameter. Agents are used to select actions that reduce ALE and \(\:S{D}_{LE}\) considering these constraints. The reward function \(\:{R}_{t}\) is used to guide the agents to minimize ALE and the variability of localization error \(\:S{D}_{LE}\). It quantifies the effectiveness of an action \(\:{A}_{t}\) taken in state \(\:{S}_{t}\) and it is mathematically formulated as follows
$$\:{R}_{t}=-\left(\varDelta\:LE+w\cdot\:\varDelta\:S{D}_{LE}\right)$$
(10)
where \(\:\varDelta\:LE=L{E}_{t+1}-L{E}_{t}\) indicates the change in ALE after applying the action \(\:{A}_{t}\). \(\:S{D}_{LE}=S{D}_{L{E}_{t+1}}-S{D}_{L{E}_{t}}\) indicates the change in the standard deviation of localization error. \(\:w\) indicates the weight parameter that balances the contributions of ALE and \(\:S{D}_{LE}\) to the reward. Agents are incentivized to minimize both \(\:\varDelta\:LE\) and \(\:\varDelta\:S{D}_{LE}\) leading to improved localization accuracy and consistency. In reinforcement learning, Q-value function \(\:Q\left({S}_{t},{A}_{t}\right)\) estimates the cumulative reward for an agent considering action \(\:{A}_{t}\) in state\(\:\:{S}_{t}\). It is updated iteratively using the Bellman equation which is mathematically expressed as follows
$$\:Q\left({S}_{t},{A}_{t}\right)\leftarrow\:Q\left({S}_{t},{A}_{t}\right)+\alpha\:\left[{R}_{t}+\gamma\:Q\:\left({S}_{t+1},A\right)-Q\left({S}_{t},{A}_{t}\right)\right]$$
(11)
where \(\:\alpha\:\) indicates the learning rate, \(\:\gamma\:\) indicates the discount factor. \(\:{R}_{t}\) indicates the immediate reward which is obtained for acting \(\:{A}_{t}\) in state \(\:{S}_{t}\). \(\:Q\:\left({S}_{t+1},A\right)\) indicates the maximum expected reward achievable from the next state \(\:\left({S}_{t+1}\right)\). This update rule allows the agents to learn optimal policies by iteratively refining their Q-value estimates based on experience. The policy \(\:\pi\:\left({S}_{t}\right)\) is used to define the probability of selecting action \(\:{A}_{t}\) given state \(\:{S}_{t}\). To balance exploration and exploitation an epsilon-greedy policy is used and the condition is mathematically formulated as
$$\:{A}_{t}=\{Random\:Action\:if\in\:>random\left(\text{0,1}\right)\:arg\:{max}_{A}Q\left({S}_{t},A\right)\:otherwise\:$$
(12)
where \(\:\epsilon\) indicates the exploration probability which gradually reduced over time to favor exploitation. \(\:random\) indicates a random number and its range is given as [0,1].
During training, all the agents share their experiences with a centralized system which further evaluates the collective actions and updates the shared Q-value function. However, during execution each agent operates independently using its learned policy to take actions. This decentralized execution ensures scalability and efficiency in large WSNs. The centralized Q-value function during training is mathematically formulated as
$$\:V\left({S}_{t}\right)=E\left[{\sum\:}_{k=0}^{\infty\:}{\gamma\:}^{k}{R}_{t+k}|{S}_{t}\right]$$
(13)
where \(\:V\left({S}_{t}\right)\) indicates the value function which estimates the long-term reward for the state \(\:\left({S}_{t}\right)\). \(\:E\) indicates the expected value operator averaging over possible future trajectories. Once trained the MARLF predicts ALE for any given state \(\:{S}_{t}\) using the learned Q-value function which is mathematically formulated as
$$\:L{E}_{pred}={f}_{Q}\left({S}_{t},{A}_{t}^{*}\right)$$
(14)
where \(\:{A}_{t}^{*}=argarg\:Q\:\:\left({S}_{t},A\right)\) which indicates the optimal action for the state \(\:{S}_{t}\) determined from the learned policy. \(\:{f}_{Q}\) indicates the prediction model derived from the Q-values. This prediction enables real-time adjustment of WSN parameters to minimize ALE dynamically. Further to attain improved prediction performance, the parameters of the MARL algorithm is optimized using Golden Jackal Optimization. The proposed model complete overview is presented in Fig. 1.
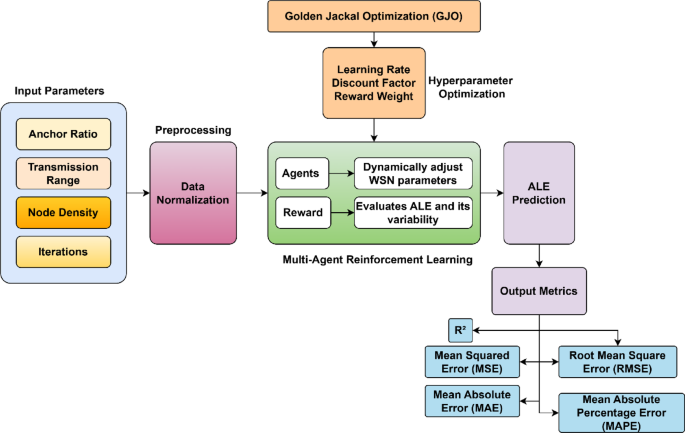
Golden jackal optimization (GJO)
GJO algorithm plays a crucial role in the proposed framework by optimizing the hyperparameters of the MARL model, including the learning rate, discount factor, and reward weights, which are vital for effective policy learning and faster convergence. Inspired by the social hunting behavior of golden jackals, GJO balances exploration and exploitation through adaptive position updates and leader-following mechanisms, enabling the model to avoid local optima and improve search efficiency. Additionally, GJO introduces random exploration strategies when progress stagnates, ensuring diverse solution searches and enhancing the generalization capability of the model. This integration accelerates convergence, improves localization accuracy, and optimizes ALE predictions, outperforming traditional static or grid search-based parameter tuning methods.
The metaheuristic GJO algorithm is framed based on the golden jackals social hunting behavior. In the proposed work GJO is incorporated with the MARL for optimizing the hyperparameters such as learning rate \(\:\alpha\:\), discount factor \(\:\gamma\:\), and reward weight \(\:w\). First the population of candidate solutions is initialized. Each solution represents a set of hyperparameters \(\:X=\{{X}_{1},{X}_{2},\dots\:,{X}_{n}\}\) in which \(\:n\) indicates the number of jackals in the population, \(\:{X}_{i}=\left[{\alpha\:}_{i},{\gamma\:}_{i},{w}_{i}\right]\) indicates the candidate solution representing the hyperparameters. Each hyperparameter is randomly initialized within predefined boundaries which are formulated as follows
$$\:\alpha\:\in\:\left[{\alpha\:}_{min},{\alpha\:}_{max}\right]\hspace{1em}$$
(15)
$$\:\gamma\:\in\:\left[{\gamma\:}_{min},{\gamma\:}_{max}\right]\hspace{1em}$$
(16)
$$\:w\in\:\left[{w}_{min},{w}_{max}\right]$$
(17)
where \(\:min,max\) indicates the allowable ranges for each hyperparameter. Further each candidate solution \(\:{X}_{i}\) is evaluated based on its fitness which is derived from the performance of the MARL. The fitness function \(\:F\left({X}_{i}\right)\) is mathematically formulated as follows
$$\:F\left({X}_{i}\right)=\frac{1}{1+MAE\left({X}_{i}\right)}$$
(18)
where \(\:MAE\left({X}_{i}\right)\) indicates the mean absolute error obtained when MARL which is trained using the hyperparameters in \(\:{X}_{i}\). \(\:F\left({X}_{i}\right)\) indicates the fitness score. The lower MAE results in a higher fitness value and vice versa. The major goal of the GJO algorithm is to maximize the fitness score effectively minimizing the prediction error of the MARL. The best solution in the current population is considered as the leader and it is identified based on the highest fitness score. Mathematically this process is formulated as follows
$$\:{X}_{leader}=argarg\:F\:\:\left({X}_{i}\right)$$
(19)
The leader represents the most promising set of hyperparameters in the current iteration. Golden Jackals use social and adaptive behaviors to refine their positions. Each jackal \(\:{X}_{i}\) updates its position based on the leader \(\:{X}_{leader}\) using the following Eq.
$$\:{X}_{i}^{t+1}={X}_{leader}+\beta\:\cdot\:\left({X}_{leader}\:-\:{X}_{i}^{t}\right)$$
(20)
where \(\:{X}_{i}^{t+1}\) Updated position of the \(\:{i}^{th}\) jackal at iteration \(\:t+1\). \(\:{X}_{leader}\) indicates the position of the leader at iteration \(\:t.{X}_{i}^{t}\) indicates the position of the \(\:{i}^{th}\) jackal at iteration \(\:t\). \(\:\beta\:\) indicates the dynamic control parameter that adjusts the magnitude of the update, defined as:
$$\:\beta\:=r\cdot\:sinsin\:\left(\frac{\pi\:}{2}\cdot\:iteration\_ratio\right)\:$$
(21)
where \(\:r\) indicates the random value in \(\:\left[\text{0,1}\right]\) to introduce randomness in the update.
$$\:iteration\_ratio=\frac{current\_iteration}{max\_iterations}$$
(22)
The normalized iteration counts to ensure gradual convergence. This position update allows jackals to follow the leader while maintaining diversity through random components.
To balance global exploration and local exploitation, GJO incorporates adaptive behaviors. When the fitness values stagnate, jackals introduce random exploration:
$$\:{X}_{i}^{t+1}={X}_{leader}+\epsilon\cdot\:rand$$
(23)
where \(\:\epsilon\) indicates the exploration factor which controls the magnitude of random movements. \(\:rand\) indicates a random value sampled from \(\:\left[-\text{1,1}\right]\). This process ensures that the algorithm explores the search space broadly while exploiting the current leader’s knowledge. In GJO, the hunting strategy is dynamically adapted based on the optimization progress. As the iteration increases jackals focus more on refining solutions around the leader and reducing the randomness in position updates. Mathematically this process is formulated as
$$\:{X}_{i}^{t+1}={X}_{leader}+\lambda\:\cdot\:rand\left(-\:\left|{X}_{i}^{t}\right|,\left|{X}_{i}^{t}\right|\right)$$
(24)
where \(\:\lambda\:\) is a parameter that decreases with each iteration to shift from exploration to exploitation. This adaptation allows the algorithm to transition from a global search to a local refinement phase. The optimization process continues until the termination criteria. The fitness values converge, i.e., the difference between the best fitness values in consecutive iterations falls below a threshold. Mathematically it is formulated as follows.
$$\:\left|F\left({X}_{leader}^{t+1}\right)-F\left({X}_{leader}^{t}\right)\right|
(25)
In the final convergence stage, final leader \(\:{X}_{leader}\) represents the optimal set of hyperparameters for the MARL. The optimized hyperparameters \(\:{\alpha\:}^{*},{\gamma\:}^{*},{w}^{*}\) are extracted from the final leader as follows
$$\:{X}_{leader}=\left[{\alpha\:}^{*},{\gamma\:}^{*},{w}^{*}\right]$$
(26)
These parameters are used to configure the MARL and ensure optimal performance in minimizing localization error and its variability. The process flow of GJO is presented in Fig. 2 in detail.
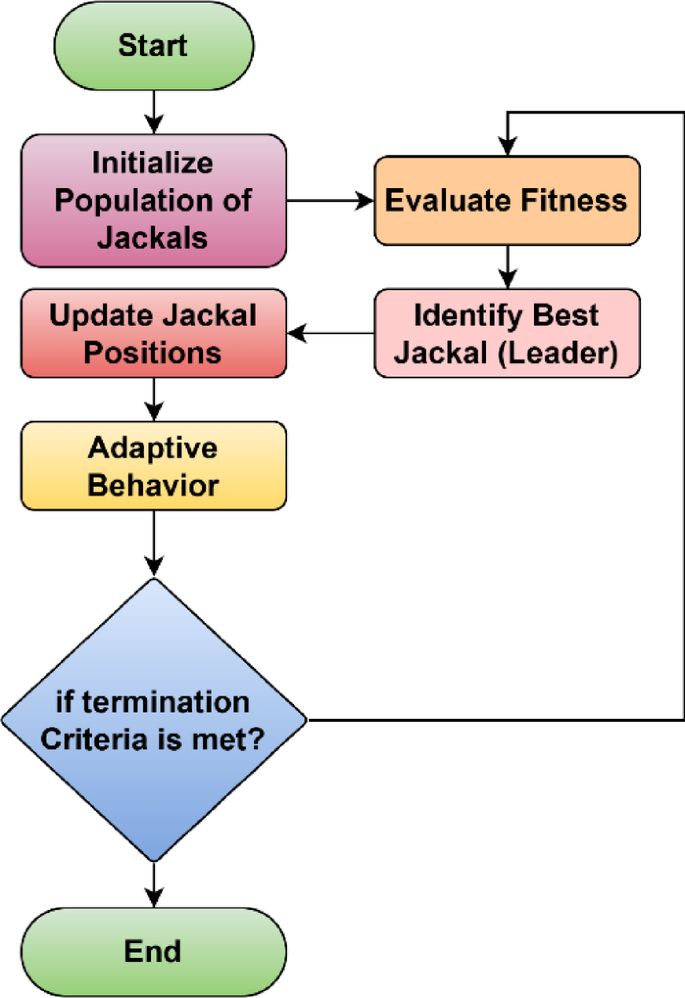
Golden Jackal Optimization.
The selection of the GTO in this study is based on its proven ability to navigate complex, high-dimensional search spaces and avoid premature convergence—a common limitation in classical optimization algorithms such as Genetic Algorithm, PSO, or Ant Colony Optimization. GTO mimics the intelligent foraging and group behavior of gorillas, allowing it to switch dynamically between exploration and exploitation phases. This characteristic makes it particularly well-suited for tuning hyperparameters in non-convex error surfaces, as found in deep learning models trained on noisy and nonlinear WSN data. Unlike PSO, which may stagnate in local optima, or GA, which often requires higher computational resources for convergence, GTO balances convergence speed with solution diversity, improving global optimality. Furthermore, its capability to adaptively update the solution based on multiple leaders within the population enhances robustness in dynamic environments. These features align well with the requirements of WSN localization error prediction, where model accuracy depends heavily on fine-tuned parameters in variable network conditions. The effectiveness of GTO is validated in this study through significant performance gains across all evaluated metrics compared to baseline models.
The objective function used in the GTO optimization framework is designed to minimize the prediction error of the AGRU model in the context of localization error estimation. The decision variables are the key hyperparameters of the AGRU model: the number of hidden units h∈[32,256], the learning rate η∈[0.0001,0.01], the batch size b∈{16,32,64,128}, and the number of training epochs e∈[50,200]. The domain boundaries for these parameters are set based on empirical knowledge and stability considerations for deep learning model training. The objective function to be minimized is the Root Mean Squared Error (RMSE) between the predicted and actual localization errors on the validation set, defined as:
$$\:Objective:\underset{\theta\:}{\text{min}}RMSE=\sqrt{\frac{1}{n}\sum\:_{i=1}^{n}(\widehat{{y}_{i}}-{y}_{i}{)}^{2}}$$
(27)
In Eq. (27), θ represents the set of hyperparameters being optimized, \(\:\widehat{{y}_{i}}\) is the predicted error, and \(\:{y}_{i}\) is the actual error. Constraints applied include maintaining model convergence within a fixed training time and ensuring that no parameter exceeds predefined bounds to prevent overfitting or computational inefficiency. The GTO algorithm iteratively evaluates candidate solutions (sets of hyperparameters), updating them based on the collective behavior of the gorilla troop until the optimal configuration yielding the lowest RMSE is found.
Average localization error (ALE) prediction
The ALE Prediction step utilizes the optimized MARL and the tuned hyperparameters from Golden Jackal Optimization (GJO) to accurately predict the ALE in a WSN. The ALE prediction process begins by defining the WSN input state which includes the network configuration and environmental conditions. The normalized input state is provided as the input to the trained MARLF. Each agent in the MARLF selects an action \(\:{A}_{t}\) based on the input state \(\:{S}_{t}\) to dynamically adjust the WSN parameters. The optimal action is determined by the Q-value function learned during training which is formulated as follows.
$$\:{A}_{t}^{*}=argarg\:Q\:\:\left({S}_{t},A\right)$$
(28)
where \(\:{A}_{t}^{*}\) indicates the optimal action at time \(\:t\) for state \(\:{S}_{t}\). \(\:Q\left({S}_{t},A\right)\) indicates the Q-value function which predicts the cumulative reward of acting \(\:A\) in state \(\:{S}_{t}\). The action \(\:{A}_{t}^{*}\) represents the adjustments to WSN parameters
$$\:{A}_{t}^{*}=\left[\varDelta\:{A}_{r},\varDelta\:{T}_{r},\varDelta\:{N}_{d},\varDelta\:{I}_{t}\right]$$
(29)
The Q-value function incorporates the optimized hyperparameters \(\:{\alpha\:}^{*}\), \(\:{\gamma\:}^{*}\), and \(\:{w}^{*}\) from GJO to ensure precise action selection. Further the reward function, learned during MARLF training, ensures that the actions chosen minimize both ALE and its variability. The reward is defined as
$$\:{R}_{t}=-\left(\varDelta\:LE+{w}^{*}\cdot\:\varDelta\:S{D}_{LE}\right)$$
(30)
where \(\:{R}_{t}\) indicates the reward for acting \(\:{A}_{t}^{*}\) in state \(\:{S}_{t}\). \(\:\varDelta\:LE=L{E}_{t+1}-L{E}_{t}\) indicates the change in ALE after applying the action \(\:{A}_{t}^{*}\). \(\:\varDelta\:S{D}_{LE}=S{D}_{L{E}_{t+1}}-S{D}_{L{E}_{t}}\) indicates the change in the standard deviation of localization error. \(\:\left({w}^{*}\right)\) indicates the weight parameter for balancing the contributions of ALE and variability, optimized through GJO. By maximizing the reward, the agents ensure that the predicted adjustments result in minimized ALE and stabilized localization error variability.
The predicted ALE \(\:\left(L{E}_{pred}\right)\) is directly obtained from the optimal Q-value corresponding to the state \(\:{S}_{t}\) and action \(\:{A}_{t}^{*}\)
$$\:L{E}_{pred}={f}_{Q}\left({S}_{t},{A}_{t}^{*}\right)$$
(31)
where \(\:L{E}_{pred}\) indicates the predicted average localization error for the given WSN configuration. \(\:{f}_{Q}\) indicates the ALE prediction model derived from the Q-value function \(\:Q\left({S}_{t},{A}_{t}\right)\). This equation represents the learned relationship between the WSN parameters, the chosen actions, and the resulting ALE. The Q-value function captures the cumulative effect of WSN parameter adjustments on ALE over time.
To improve ALE prediction in dynamic WSN environments, the model incorporates temporal dependencies between successive states. The temporal Q-value update is defined as
$$\:Q\left({S}_{t},{A}_{t}\right)\leftarrow\:Q\left({S}_{t},{A}_{t}\right)+{\alpha\:}^{*}\left[{R}_{t}+{\gamma\:}^{*}Q\:\left({S}_{t+1},A\right)-Q\left({S}_{t},{A}_{t}\right)\right]$$
(32)
where \(\:{\alpha\:}^{*}\) is the optimized learning rate, controlling the step size for updating Q-values. \(\:{\gamma\:}^{*}\) indicates the optimized discount factor which is used to weigh the importance of future rewards. \(\:{S}_{t+1}\) indicates the next state after applying the action \(\:{A}_{t}\). This temporal Q-value formulation ensures that the model learns to predict ALE accurately by considering the sequential nature of parameter adjustments.
The ALE prediction model is trained to minimize the error between the predicted ALE \(\:\left(L{E}_{pred}\right)\) and the true ALE \(\:\left(L{E}_{true}\right)\). The loss function is defined as
$$\:L=\frac{1}{N}{\sum\:}_{i=1}^{N}{\left(L{E}_{i,true}-L{E}_{i,pred}\right)}^{2}+\lambda\:\cdot\:Var\left(L{E}_{pred}\right)$$
(33)
where \(\:L\) indicates the total loss. \(\:N\) indicates the total number of data points in the training set, \(\:L{E}_{i,true}\) indicates the true ALE for the \(\:{i}^{th}\) data point. \(\:L{E}_{i,pred}\) indicates the predicted ALE and \(\:Var\left(L{E}_{pred}\right)\) indicates the variance of the predicted ALE values. \(\:\lambda\:\) indicates the regularization parameter which is used to control the trade-off between prediction accuracy and stability. Minimizing \(\:L\) ensures that the ALE predictions are accurate and consistent across WSN configurations. The summarized pseudocode for the proposed adaptive ALE prediction model using MARL-GJO is presented as follows.
|
Algorithm 1: Adaptive Average Localization Error Prediction using MARL-GJO Framework |
|---|
|
Input: \(\:{S}_{t}=\left[{A}_{r},{T}_{r},{N}_{d},{I}_{t}\right]\), \(\:{\alpha\:}_{min},{\alpha\:}_{max}\), \(\:{\gamma\:}_{min},{\gamma\:}_{max}\), \(\:{w}_{min},{w}_{max}\), \(\:L{E}_{i,true}\), Population size \(\:\left(n\right)\), maximum iterations \(\:\left(Tmax\right)\), |
|
Output: optimized hyperparameters \(\:{\alpha\:}^{*}\), \(\:{\gamma\:}^{*}\), and \(\:{w}^{*}\) |
|
Initialize the Population of Golden Jackals |
|
Generate an initial population of\(\:\left(n\right)\) jackals |
|
Evaluate Fitness of Each Candidate |
|
For each candidate solution\(\:{X}_{i}\) |
|
Configure the MARLF with hyperparameters\(\:\left[{\alpha\:}_{i},{\gamma\:}_{i},{w}_{i}\right]\) |
|
Train MARLF on the dataset\(\:\left\{\left({S}_{t},L{E}_{true}\right)\right\}\) by minimizing the loss function |
|
\(\:L=\frac{1}{N}{\sum\:}_{i=1}^{N}{\left(L{E}_{i,true}-L{E}_{i,pred}\right)}^{2}+{w}_{i}\cdot\:Var\left(L{E}_{pred}\right)\) |
|
Compute the fitness\(\:F\left({X}_{i}\right)=\frac{1}{1+MAE\left({X}_{i}\right)}\) |
|
To Identify the Leader |
|
Select the best-performing jackal (leader) based on the highest fitness \(\:{X}_{leader}=argF\:\:\left({X}_{i}\right)\) |
|
Update the position for each iteration\(\:(t=\text{1,2},\dots\:,{T}_{max})\) |
|
for each jackal\(\:\left({X}_{i}\right)\) |
|
Update the position based on the leader \(\:{X}_{i}^{t+1}={X}_{leader}+\beta\:\cdot\:\left({X}_{leader}-{X}_{i}^{t}\right)\) |
|
If fitness values stagnate, add random exploration \(\:{X}_{i}^{t+1}={X}_{leader}+\epsilon\cdot\:random\left(-\text{1,1}\right)\) |
|
Evaluate the fitness of the updated positions\(\:{X}_{i}^{t+1}\) \(\:F\left({X}_{i}^{t+1}\right)=\frac{1}{1+MAE\left({X}_{i}^{t+1}\right)}\) |
|
Update the leader if a better solution is found \(\:{X}_{leader}=argF\:\:\left({X}_{i}^{t+1}\right)\) |
|
Check convergence criteria |
|
\(\:\left|F\left({X}_{leader}^{t+1}\right)-F\left({X}_{leader}^{t}\right)\right| |
|
If convergence met |
|
End |
|
Else |
|
Use the final leader\(\:{X}_{leader}=\left[{\alpha\:}^{*},{\gamma\:}^{*},{w}^{*}\right]\) |
|
Train the MARLF by updating the Q-value function iteratively |
|
\(\:\left({S}_{t},{A}_{t}\right)\leftarrow\:Q\left({S}_{t},{A}_{t}\right)+{\alpha\:}^{*}\left[{R}_{t}+{\gamma\:}^{*}Q\:\left({S}_{t+1},A\right)-Q\left({S}_{t},{A}_{t}\right)\right]\) |
|
The reward function is\(\:{R}_{t}=-\left(\varDelta\:LE+{w}^{*}\cdot\:\varDelta\:S{D}_{LE}\right)\) |
|
To Predict ALE For a given WSN configuration\(\:\left({S}_{t}\right)\), |
|
Compute the optimal action\(\:{A}_{t}^{*}=argarg\:Q\:\:\left({S}_{t},A\right)\) |
|
Use the trained Q-value function to predict\(\:L{E}_{pred}={f}_{Q}\left({S}_{t},{A}_{t}^{*}\right)\) |
|
End |
|
End |
|
End |




