This study uses an improved version of a metaheuristic, called Osprey Optimizer (OO). We have chosen the Osprey Optimizer in this study for its unique ability to search and robust global optimization capabilities, which are imperative for the fine-tuning of deep-learning models such as the MobileNetV3 assigned to complex tasks like land-use classification. The Osprey Optimizer mimicking the hunting strategies of ospreys combines exploration (searching for prey) and exploitation (capturing and transporting prey away), thus ensuring a good compromise between searching for new regions while refining promising solutions. This in turn results in excellent convergence speed and precision when optimizing hyperparameters and weights of neural networks.
In addition to the limited number of control parameters, the Osprey Optimizer method exhibits a greater stability than other metaheuristic algorithms, consequently making it computationally efficient and less prone to overfitting. This further adds to the justification of the novelty and effectiveness of the proposed GOO technique on the enhancement of land-use classification accuracy over traditional optimization techniques, all the while since remaining computationally inexpensive. In the following, the recommended algorithm and mathematical model have been described.
Inspiration
The Osprey is named fish, sea, and river hawk. It is an animal that nourishes different kinds of fishes and inhabits during night time. The wingspan, weight, and length of the individuals are, in turn, between 127 and 180 cm, 0.9 and 2.1 kg, and 50 and 66 cm. The various attributes of these animals are expressed subsequently. The areas in the upper appear to be brilliant brown, while the breast appears to be white with some brown specks visible on it. The portion on the underside is all white. There have been reports of a white head covered in black from the eyes down to the neck. Then, the individual’s nictitating membrane appears to be bright blue, and its iris is between golden and brown. The beak, feet, and talons of these individuals are all black. These individuals’ wings and tail are, in turn, narrow-long and short.
The chief diet of these animals is fish. The animal often hunts live fish that are between 35 and 25 cm in length and between 300 and 150 g in weight. However, it can catch fish weighing between 2 kg and 50 g. These creatures have extraordinary eyesight, enabling them to identify and locate objects lower the surface of the water, even while they are flying 10–40 m in the air. Then, they approach the target and dive into the water to catch them. Once the individuals catch the prey, they move the target to the nearest rock and nourish it. Of course, this intelligent behavior has been considered a foundation to develop a novel algorithm. Thus, mathematical model of the individuals’ smart behavior is employed while developing the recommended optimizer. Moreover, it has been completely expressed below.
Mathematical model
The way of initializing the optimizer is expressed here. Then, the individual’s situation improvement is described in two various steps, including exploitation and exploration, according to replication of the individuals’ natural manners.
-
(A)
Initialization.
The recommended optimizer is on the basis of the population that demonstrates strong capabilities to offer a proper problem solver according to search supremacy in problem space through an iteration procedure. Each animal has a decisive role determining problem variables according its situation in the solution space. Therefore, each individual is a candidate solution statistically made employing a vector. Each of these individuals create the population of the optimizer replicated by employing the matrix presented subsequently. In the beginning, the situations of these individual in the solution space are initialized in a stochastic manner employing the formula presented in the following:
$$Y={\left[ {\begin{array}{*{20}{c}} {{Y_1}} \\ \vdots \\ {\begin{array}{*{20}{c}} {{Y_j}} \\ {\begin{array}{*{20}{c}} \vdots \\ {{Y_N}} \end{array}} \end{array}} \end{array}} \right]_{N \times k}}={\left[ {\begin{array}{*{20}{c}} {{Y_{1,1}}}& \cdots &{\begin{array}{*{20}{c}} {{Y_{1,i}}}& \cdots &{{Y_{1,k}}} \end{array}} \\ \vdots & \ddots &{\begin{array}{*{20}{c}} \vdots &{~~~~~ \vdots }&{~~~ \vdots ~~} \end{array}} \\ {\begin{array}{*{20}{c}} {{Y_{j,1}}} \\ \vdots \\ {{Y_{N,1}}} \end{array}}&{\begin{array}{*{20}{c}} \cdots \\ {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} \\ \cdots \end{array}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{Y_{j,i}}} \\ \vdots \\ {{Y_{N,i}}} \end{array}}&{\begin{array}{*{20}{c}} { \cdots ~~} \\ { \ddots ~~~} \\ \cdots \end{array}~}&{\begin{array}{*{20}{c}} {{Y_{j,k}}} \\ \vdots \\ {{Y_{N,k}}} \end{array}} \end{array}} \end{array}} \right]_{N \times k}},$$
(8)
$${Y_{j,i}}=l{b_i}+{r_{j,i}} \times \left( {u{b_i} – l{b_i}} \right),~j=1,~2,…,~k,$$
(9)
where, population of matrix is demonstrated by Y, the \({j^{th}}\) individual is indicated by \({Y_j}\) that is famous for being candidate solution, the \({i^{th}}\) dimension is denoted by \({Y_{j,i}}\), the quantity of candidates is represented by N, the number of issue variables is displayed by k, and the stochastic number are illustrated by \({r_{j,i}}\) that are in the range of [0, 1]. Furthermore, the lower and upper bounds of the \({i^{th}}\) issue variable are represented by \(l{b_i}\) and \(u{b_i}.\)
Evaluating the objective function is probable since each individual is imagined as candidate solution. A vector is probably able to illustrate the value assessed for the issue’s fitness function.
$$G={\left[ {\begin{array}{*{20}{c}} {{G_1}~} \\ \vdots \\ {\begin{array}{*{20}{c}} {{G_j}} \\ {\begin{array}{*{20}{c}} \vdots \\ {{G_N}} \end{array}} \end{array}} \end{array}} \right]_{N \times 1}}={\left[ {\begin{array}{*{20}{c}} {G\left( {{Y_1}} \right)} \\ \vdots \\ {\begin{array}{*{20}{c}} {G\left( {{Y_j}} \right)} \\ \vdots \\ {G\left( {{Y_N}} \right)} \end{array}} \end{array}} \right]_{N \times 1}},$$
(10)
Here, the vector of objective function values is depicted G; additionally, the achieved objective function value of the \({j^{th}}\) individual is illustrated by \({G_j}.\)
The evaluated values of the objective funion are chief prerequisite to evaluate the quality of the candidate solutions. Thus, the best value achieved for the objective function illustrates the best candidate solution. in addition, the worst value attained for the objective function depicts the worst candidate solution. Once the situation of these individuals in the solution space is enhanced in each iteration, the best candidate solution must be enhanced too.
-
(B)
Stage 1: Identification of situation and catching the target (global search).
These individuals have been found to be giant hunter that are able to identify the situation of the prey lower the water, since they a powerful eyesight. When the situation of the target is identified under the water, the individual dives into the water to catch it. The starting step population enhancement in the present optimizer is replicated based on the natural behavior of these individuals. replicating the attacking manner of the individual can alter the individuals’ situation that enhances the global search capability of the optimizer to recognize optimal zone and flee from local optima.
The prey is capable of determining the situation of the individuals in the search space that their objective function values are really high. The set of the targets for the candidates is replicated by the formula presented in the following:
$$G{p_j}=\left[ {{Y_z}|z \in \left[ {1,{\text{~}}2,…,{\text{~}}N} \right] \wedge {G_z}<{G_j}} \right] \cup \left[ {{Y_{best}}} \right],$$
(11)
where, the situation of the prey for the \({j^{th}}\) candidate is denoted by \(G{p_j}\); moreover, the best candidate solution is demonstrated by \({Y_{best}}.\)
Each candidate detects the target’s situation and attacks it. According to the replication of the candidate’s movement toward the target, the new situation of the candidate is calculated by employing Eq. (18). When, the new situation improves the benchmark function, it replaces the previous situation of the candidate according to Eq. (19).
$$Y_{{j,i}}^{{P1}}={Y_{j,i}}+{r_{j,i}} \times \left( {H{G_{j,i}} – {I_{j,i}}} \right) \times {Y_{j,i}},$$
(12-a)
$$Y_{{j,i}}^{{P1}}=\left\{ {\begin{array}{*{20}{c}} {Y_{{j,i}}^{{P1}},~l{b_i} \leqslant Y_{{j,i}}^{{P1}} \leqslant u{b_i};} \\ {l{b_i},~Y_{{j,i}}^{{P1}}
(12-b)
$${Y_j}\left\{ {\begin{array}{*{20}{c}} {Y_{j}^{{p1}},~G_{j}^{{P1}}<{G_j}~} \\ {{Y_j},~else,~~~~~~~~~~~~~} \end{array}} \right.$$
(13)
Here, the new situation of the \({j^{th}}\) candidate is represented by \(Y_{j}^{{P1}}\) on the basis of the starting step of the optimizer, the \({i^{th}}\) dimension is depicted by \(Y_{{j,i}}^{{P1}}\), the fitness function value is \(G_{j}^{{P1}}\), the selected prey of the \({j^h}\) candidate is displayed by \(H{G_j}\), the \({i^{th}}\) dimension is represented by \(H{G_{j,i}}\), \({r_{j,i}}\) is a random quantity that is in the range of [0, 1], and \({I_{j,i}}\) has been regarded as a stochastic number that is between 1 and 2.
-
(C)
Stage 2: Taking the target to a proper situation (local search).
When the candidate catches a prey, it takes it to a proper situation to make sure it is safe, then the candidate nourishes the target. The following step of the population upgrade is replicated according to the natural behaviors of the candidates. The replication of taking the prey to a proper situation alters the situation candidate as well. Hence, it enhances the optimizer’s capability in local search and leads to convergence to better problem solver.
While designing the OOA, a new situation is calculated by employing Eq. (14) to replicate the natural manners of these candidates. In fact, this situation is proper to nourish the target. Afterwards, the new situation replaced by the previous one according to the Eq. (15) below when its value of fitness function improves.
$$Y_{{j,i}}^{{p2}}={Y_{j,i}}+\frac{{l{b_i}+r \times \left( {u{b_i} – l{b_i}} \right)}}{t},~j=1,~2,…,~N,~i=1,~2,…,~k,~t=1,~2,…,~T,$$
(14-a)
$$Y_{{j,i}}^{{p2}}=\left\{ {\begin{array}{*{20}{c}} {Y_{{j,i}}^{{p2}},~l{b_i} \leqslant Y_{{j,i}}^{{p2}} \leqslant u{b_i};} \\ {l{b_i},~Y_{{j,i}}^{{p2}}
(14-b)
$${Y_j}=\left\{ {\begin{array}{*{20}{c}} {Y_{j}^{{P2}},~G_{j}^{{P2}}<{G_j};} \\ {{Y_j},~else,~~~~~~~~~~~~~} \end{array}} \right.$$
(15)
where, the new situation of the \({j^{th}}\) candidate is demonstrated by \(Y_{j}^{{p2}}\) on the basis of the second step of the optimizer, its \({i^{th}}\) dimension is displayed by \(Y_{{j,i}}^{{p2}}\), the random quantity is indicated by \({r_{j,i}}\) that is in the range of [0, 1], the fitness function value is represented via \(G_{j}^{{P2}}\), the total quantity of iteration is shown by T, and the quantity of iterations is signified by t.
The recommended optimizer is on the basis of iteration. The optimizer’s first iteration has been achieved by enhancing the situation of each candidate on the basis of the second and first phase. Next, the best individual solution is enhanced after comparing different benchmark function values. Subsequently, the suggested optimizer begins another iteration with new situation of each animal. In addition, the enhancement process of the optimizer carries on by the ultimate iteration in accordance with Eqs. (11) to (15). Consequently, when the optimizer is completely carried out, the it illustrates the best candidate as a problem solver.
Osprey optimizer based on information exchange and greedy search
The recommended algorithm possesses a particular global search formula; however, the value of z is really minor that leads to a low possibility of implementing a global search and constrained local search ability. To tackle the aforementioned problem, the extra global search is required for the recommended optimizer. It assists the optimizer in overcoming the local minima and enhancing the diversity of the candidates. Thus, an adjustive decision-making technique has been proposed in the current study for determining the fact that if it is urgent to explore employing formulas of data exchange. The particular operations have been described in the following.
Initially, the optimizer’s fitness value must be calculated once the updating the situation of the individuals has been accomplished. If the novel value of fitness is lower than the previous one, then information must be exchanged between the candidates. Else, the upgraded situation and value of fitness must be retained. The model of information exchange has been calculated in the following way:
$${J_j}={Y_S}+{r_2} \times \left( {{Y_{best}} – {Y_i}} \right)+{r_3} \times \left( {{Y_c} – {Y_d}} \right)$$
(16)
here, \({r_3}\) and \({r_2}\) have been found to be stochastic numbers that have been distributed in a uniform manner in the range of -0.5 and 0.5, the optimum situation of the candidates has been displayed by \({Y_{best}}\), and the situation of the candidate that has been stochastically chosen after updating the situation has been demonstrated by \({Y_d}\) and \({Y_c}\). The present position of the candidates has been depicted by \({Y_i}\), the candidate’s position that has been produced by a greedy stochastic opposition acquiring has been illustrated by \({Y_S}\). The particular implementations have been described in the subsequent manner:
$${X_S}=\left\{ {\begin{array}{*{20}{c}} {{Y_j}~~~~~if~~~~~f\left( {{Y_j}} \right)
(17)
here, the opposite candidate that has been gained through \({Y_j}\) is displayed via \({\bar {Y}_j}\) by employing stochastic opposite mechanism of learning. The procedure is illustrated subsequently:
$${\bar {Y}_j}=\hbox{min} \left( {{Y_j}} \right)+rand \times \left( {\hbox{max} \left( {{Y_j}} \right) – {Y_j}} \right)$$
(18)
where, the minimum and maximum values of the candidates’ dimension situation have been, in turn, represented by \(\hbox{min} \left( {{Y_j}} \right)\) and \(\hbox{max} \left( {{Y_j}} \right)\), and \(rand\) has been considered a stochastic number distributed in a uniform manner in the range of 0 and 1.
Once the exchange of information has been accomplished, the novel fitness value \(f\left( {{J_j}} \right)\) must be calculated, then it must be compared with the fitness value after update of location \(f\left( {{Y_j}} \right)\). Then, \(f\left( {{J_j}} \right)\) must be employed to upgrade \({Y_j}\) if the value of fitness after exchanging the information is finer. Else, \({Y_j}\) must be disturbed for generation of a novel situation. The mode of disturbance has been displayed in the following way:
$${R_j}={Y_j} \times \left( {1+\left( {0.5 – rand} \right)} \right)$$
(19)
here, the situation of candidates after updating their situation have been displayed by \({Y_j}\), and \(rand\) that has been distributed in a uniform manner in the range of 0 and 1.
Eventually, the fitness value of the candidates must be computed after disturbance, then the greedy choice method must be employed.
$${Y_j}\left( {t+1} \right)=\left\{ {\begin{array}{*{20}{c}} {{Y_j}\left( t \right)~~~~~if~~~~~f\left( {{Y_j}} \right)
(20)
The addition of information exchange among the candidate will assist to enhance the diverse populations; moreover, the disturbance helps produce a novel situation. Hence, a finer problem solver has been gained. The greedy choice technique provides a finer problem solver for the subsequent iteration. Figure 6 shows the flowchart diagram of the GOO algorithm.
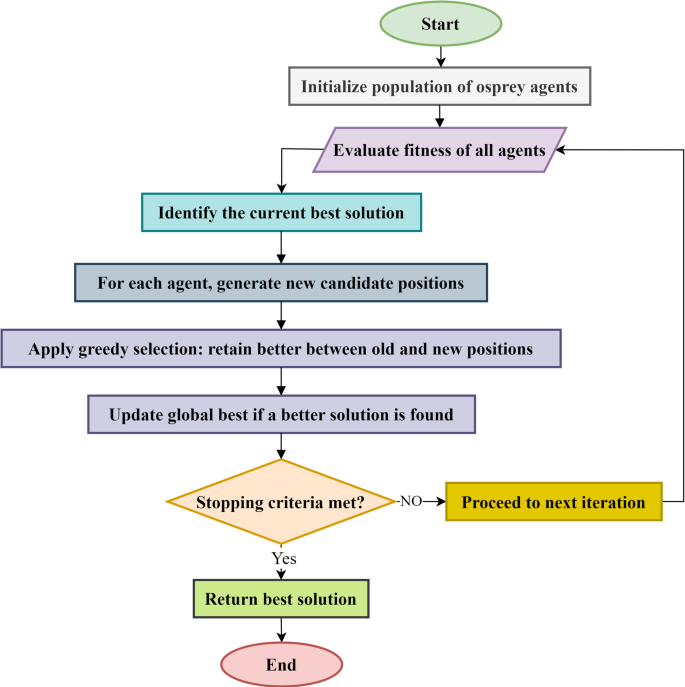
The flowchart diagram of the GOO algorithm.
Algorithm verification
This section provides an in-depth investigation of the optimization performance of the proposed Greedy Osprey Optimizer (GOO) and provide a comparative analysis with some other state of the art to show its efficiency. The employed metaheuristics including Lévy flight distribution (LFD)27, Marine Predators Algorithm (MPA)28, Reptile Search Algorithm (RSA)29, β-hill climbing (β HC)30, and non-monopolize search (NO)31.
These algorithms have been carefully designed to tackle different types of problems, providing useful information on global optimization in the continuous domain. The following table shows the parameter values used for comparison between the proposed GOO algorithm and other investigated metaheuristics. Table 1 illustrates the employed parameter values of the compared optimization algorithms.
The primary goal is to introduce a method that examines how well GOO and the other compared metaheuristics perform in solving 12 CEC-2021 benchmark problems. These problems vary in complexity and search space dimensions. The assessment included determining the mean and standard deviation values. Each algorithm was run separately 20 times, with a fixed population size of 300 and 50 agents. Here, fmean indicates mean value of the function, and fstd shows the standard deviation value. The results of this comparison are shown in Table 2.
In the first batch of problems (f1 to f3), GOO performs significantly better than the other algorithms. It consistently achieves extremely low mean values, almost close to zero, and has negligible standard deviations. This suggests that GOO is highly effective in optimizing these functions and often finds solutions very close to the global optimum. While LFD and β HC also perform reasonably well on these problems, their mean and standard deviation values are much higher than GOO, indicating less consistent performance.
For problems f4 to f6, GOO once again demonstrates its strength. Its mean values are several orders of magnitude lower than the competing algorithms, and the standard deviations are relatively low, indicating GOO’s robustness. Although LFD and RSA show some competitiveness on these problems, their performance is still not on par with GOO.
Moving on to problems f7 to f9, GOO continues to excel with exceptionally low mean and standard deviation values. While LFD and β HC show some promise on these problems, their performance is still inferior to GOO. It is worth noting that for problem f9, GOO achieves an extremely low mean value, indicating its consistent ability to find near-optimal solutions.
In the final set of problems (f10 to f12), GOO maintains its dominance with the lowest mean and competitive standard deviation values. Although LFD and RSA show some strength on these problems, particularly on f10 and f11, their performance is still overshadowed by GOO.




